A Principal Component Analysis of the Voynich Manuscript Pages showed that pages form clusters in agreement with the illustrations which appear on the same pages, or lack of them. The clusters found were
- Herbal
- Pharmaceutical
- Cosmological, Astronomical, and Astrological
- Text and Recipes
- Biological
The cluster formed by the herbal pages was larger, and overlapped the other clusters except for the one containing the biological pages. Furthermore, it contains both Currier A and B pages. It was also noted that the dividing line between Currier A and B was somewhat arbitrary.
The herbal pages were separated from the rest of the manuscript. Two text pages, f1r and f66r, are contiguous only with herbal pages and cluster similarly, so they were also included. Two other statistical techniques, minimum spanning tree and k-means clustering were then performed, to find out if there were clusters within the herbal pages. While the minimum spanning tree is unique for a given set of points, k-means clustering is something of a black art. One problem is that it is biased towards circular clusters. Usually the value of k, the number of clusters, is supplied, and the results verified visually. When run to determine k, it found a single cluster. When k was set to 2 to see if it separated Currier A and B pages, one cluster had only Currier A pages, and the other had both Currier A and B pages. When k was set to 3, the result was the similar to k=4, but with the blue and black clusters merged. The best results were obtained for k=4, when the clusters found approximately matched branches of the minimum spanning tree, but still required a few corrections. The red points correspond closely to Currier B pages.

Figure 1: PCA of herbal pages with minimum spanning tree and k=4 means clustering superimposed
I think that the red-black boundary should be between f51r and f52r, and the black-blue boundary should be between f2r and f15r. This maximizes the distances between the clusters in the spanning tree. Then, a few points should change cluster to ensure that every point in a cluster is reachable from every other point, without passing through another cluster, for example f9v should move from green to black, and f90v2, f48r, and f87v should move from red to black. This means that f48r should now be classified as Currier A, and f51r and f65v as Currier B.
The page classifications are then
| Page | Coordinates | Cluster | Corrected cluster |
| f1r | #(445.126723 570.325368) | BLACK | BLUE |
| f1v | #(395.681670 708.695406) | BLUE | BLUE |
| f2r | #(417.449659 533.266031) | BLACK | BLACK |
| f2v | #(636.038676 768.990940) | BLUE | BLUE |
| f3r | #(415.178307 749.627159) | BLUE | BLUE |
| f3v | #(394.417008 590.638530) | BLACK | BLUE |
| f4r | #(572.906637 635.736760) | BLUE | BLUE |
| f4v | #(498.278029 488.260780) | BLACK | BLACK |
| f5r | #(435.850367 504.572907) | BLACK | BLACK |
| f5v | #(709.729358 498.996359) | GREEN | GREEN |
| f6r | #(449.661434 521.527198) | BLACK | BLACK |
| f6v | #(421.432087 616.397124) | BLACK | BLUE |
| f7r | #(426.917084 618.973014) | BLACK | BLUE |
| f7v | #(538.112207 376.222930) | GREEN | GREEN |
| f8r | #(444.838058 579.048059) | BLACK | BLUE |
| f8v | #(498.612607 694.641975) | BLUE | BLUE |
| f9r | #(404.037025 599.890555) | BLACK | BLUE |
| f9v | #(614.864790 499.661984) | GREEN | BLACK |
| f10r | #(531.912656 527.163559) | BLACK | BLACK |
| f10v | #(796.634273 314.640624) | GREEN | GREEN |
| f11r | #(696.039478 357.419399) | GREEN | GREEN |
| f11v | #(414.944437 605.048796) | BLACK | BLUE |
| f13r | #(477.445237 600.226430) | BLACK | BLUE |
| f13v | #(433.636813 463.629612) | BLACK | BLACK |
| f14r | #(439.602281 424.775927) | BLACK | BLACK |
| f14v | #(550.726017 378.469010) | GREEN | GREEN |
| f15r | #(442.303593 553.612624) | BLACK | BLUE |
| f15v | #(579.316502 706.386240) | BLUE | BLUE |
| f16r | #(435.674051 397.936045) | RED | BLACK |
| f16v | #(503.900369 623.903709) | BLUE | BLUE |
| f17r | #(353.540100 636.948195) | BLACK | BLUE |
| f17v | #(383.207067 665.348579) | BLUE | BLUE |
| f18r | #(405.910030 501.079683) | BLACK | BLACK |
| f18v | #(368.740496 434.136060) | BLACK | BLACK |
| f19r | #(667.087936 432.162537) | GREEN | GREEN |
| f19v | #(675.410855 261.812036) | GREEN | GREEN |
| f20r | #(484.381392 467.213295) | BLACK | BLACK |
| f20v | #(511.886451 669.496549) | BLUE | BLUE |
| f21r | #(494.779190 617.747945) | BLUE | BLUE |
| f21v | #(666.543696 390.858814) | GREEN | GREEN |
| f22r | #(608.710192 268.102587) | GREEN | GREEN |
| f22v | #(640.090168 335.651624) | GREEN | GREEN |
| f23r | #(456.255402 404.510553) | BLACK | BLACK |
| f23v | #(364.034255 523.159434) | BLACK | BLACK |
| f24r | #(411.993407 512.420304) | BLACK | BLACK |
| f24v | #(357.263316 638.592231) | BLACK | BLUE |
| f25r | #(623.131389 243.053694) | GREEN | GREEN |
| f25v | #(870.000000 31.141652) | GREEN | GREEN |
| f26r | #(309.530567 278.024914) | RED | RED |
| f26v | #(263.063941 340.130946) | RED | RED |
| f27r | #(404.033502 870.000000) | BLUE | BLUE |
| f27v | #(373.623268 696.883413) | BLUE | BLUE |
| f28r | #(378.764886 483.488038) | BLACK | BLACK |
| f28v | #(566.594348 611.966289) | BLUE | BLUE |
| f29r | #(382.067280 700.882746) | BLUE | BLUE |
| f29v | #(503.396837 654.768879) | BLUE | BLUE |
| f30r | #(405.679465 506.314893) | BLACK | BLACK |
| f30v | #(649.857224 295.190235) | GREEN | GREEN |
| f31r | #(366.720562 231.497744) | RED | RED |
| f31v | #(329.784997 335.276775) | RED | RED |
| f32r | #(561.876110 333.649327) | GREEN | GREEN |
| f32v | #(763.771957 331.503884) | GREEN | GREEN |
| f33r | #(319.457646 210.057885) | RED | RED |
| f33v | #(306.695241 366.988786) | RED | RED |
| f34r | #(318.386080 297.757709) | RED | RED |
| f34v | #(298.831022 256.141837) | RED | RED |
| f35r | #(566.924863 379.411331) | GREEN | GREEN |
| f35v | #(607.497471 376.228665) | GREEN | GREEN |
| f36r | #(519.966664 501.542380) | BLACK | BLACK |
| f36v | #(567.421418 254.604115) | GREEN | GREEN |
| f37r | #(564.512222 331.254040) | GREEN | GREEN |
| f37v | #(838.653572 127.213815) | GREEN | GREEN |
| f38r | #(490.785593 339.027852) | GREEN | GREEN |
| f38v | #(625.425893 392.483603) | GREEN | GREEN |
| f39r | #(337.328635 296.067823) | RED | RED |
| f39v | #(266.430913 305.976431) | RED | RED |
| f40r | #(274.281779 251.366398) | RED | RED |
| f40v | #(317.502654 262.701289) | RED | RED |
| f41r | #(315.303466 331.543858) | RED | RED |
| f41v | #(365.378948 299.761422) | RED | RED |
| f42r | #(469.063241 731.624877) | BLUE | BLUE |
| f42v | #(418.015745 591.167212) | BLACK | BLUE |
| f43r | #(336.420431 338.549159) | RED | RED |
| f43v | #(283.714622 323.945316) | RED | RED |
| f44r | #(417.383837 518.754220) | BLACK | BLACK |
| f44v | #(419.681213 629.626465) | BLUE | BLUE |
| f45r | #(433.134427 482.745354) | BLACK | BLACK |
| f45v | #(391.519522 548.773382) | BLACK | BLACK |
| f46r | #(400.329968 369.002524) | RED | RED |
| f46v | #(353.983632 205.747946) | RED | RED |
| f47r | #(586.148836 800.013641) | BLUE | BLUE |
| f47v | #(513.568590 591.839506) | BLUE | BLUE |
| f48r | #(337.445604 416.248074) | RED | BLACK |
| f48v | #(267.637707 343.252443) | RED | RED |
| f49r | #(535.031754 521.598205) | BLACK | BLACK |
| f49v | #(504.726337 574.814090) | BLACK | BLUE |
| f50r | #(301.490083 302.433582) | RED | RED |
| f50v | #(321.918051 284.007139) | RED | RED |
| f51r | #(407.083921 365.778989) | RED | RED |
| f51v | #(549.392337 280.424928) | GREEN | GREEN |
| f52r | #(419.927660 400.870474) | RED | BLACK |
| f52v | #(467.952024 511.901153) | BLACK | BLACK |
| f53r | #(343.196037 523.644808) | BLACK | BLACK |
| f53v | #(555.100873 397.966632) | GREEN | GREEN |
| f54r | #(383.661365 537.551475) | BLACK | BLACK |
| f54v | #(390.421207 524.728171) | BLACK | BLACK |
| f55r | #(358.158223 333.723490) | RED | RED |
| f55v | #(425.331329 160.059434) | RED | RED |
| f56r | #(518.606037 567.391784) | BLACK | BLUE |
| f56v | #(593.684200 722.927991) | BLUE | BLUE |
| f57r | #(364.522344 353.863544) | RED | RED |
| f65v | #(371.481917 352.508275) | RED | RED |
| f66r | #(348.138972 357.994379) | RED | RED |
| f66v | #(360.909022 316.431757) | RED | RED |
| f87r | #(442.696329 434.549904) | BLACK | BLACK |
| f87v | #(351.495397 425.980341) | RED | BLACK |
| f90r1 | #(341.882612 548.866917) | BLACK | BLACK |
| f90r2 | #(508.938876 335.876296) | GREEN | GREEN |
| f90v2 | #(309.486772 451.262816) | RED | BLACK |
| f90v1 | #(383.315727 445.679512) | BLACK | BLACK |
| f93r | #(402.395485 515.856235) | BLACK | BLACK |
| f93v | #(306.276048 472.923469) | BLACK | BLACK |
| f94r | #(344.324124 340.544160) | RED | RED |
| f94v | #(340.275584 296.605930) | RED | RED |
| f95r1 | #(328.371128 339.651457) | RED | RED |
| f95r2 | #(340.123281 313.042428) | RED | RED |
| f95v2 | #(310.908008 273.858492) | RED | RED |
| f95v1 | #(305.218070 340.001062) | RED | RED |
| f96r | #(384.517803 472.902987) | BLACK | BLACK |
| f96v | #(427.211885 418.659423) | BLACK | BLACK |
K-means clustering was also done for the text/recipes pages and biological pages. The best results were for k=3, and no manual corrections were required.
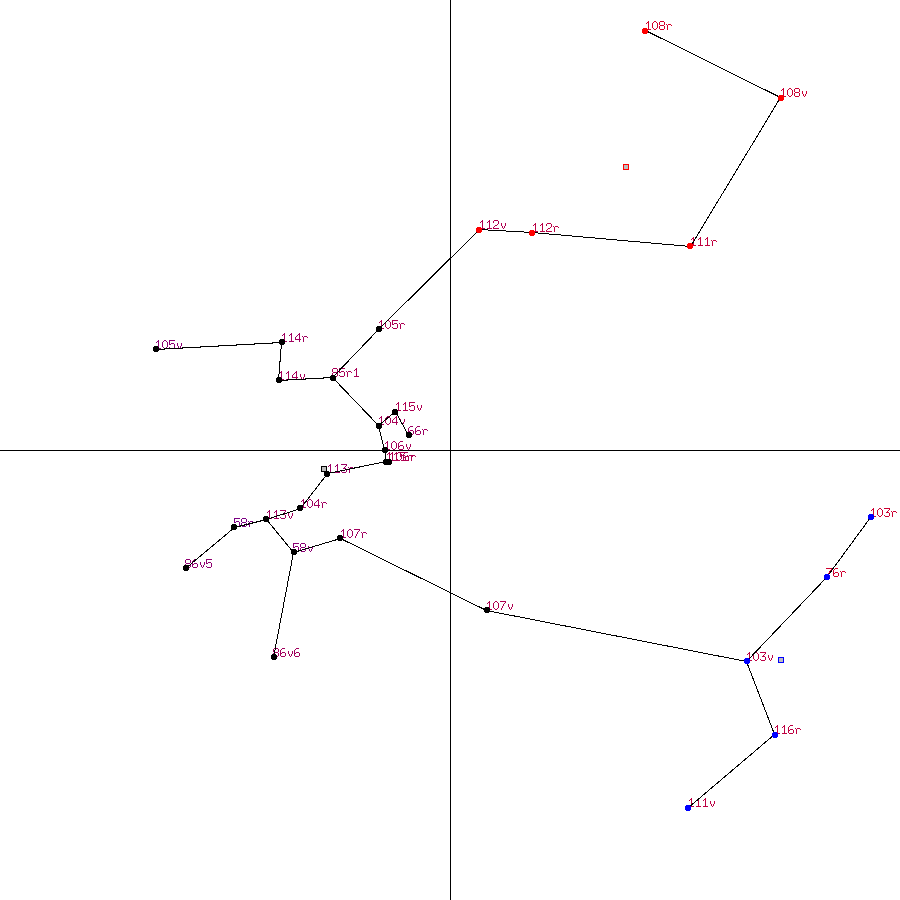
Figure 2: PCA of text/recipes pages with minimum spanning tree and k=3 means clustering superimposed
| Page | Coordinates | Cluster | Corrected cluster |
| f58r | #(233.949773 526.806531) | BLACK | BLACK |
| f58v | #(293.145622 551.840377) | BLACK | BLACK |
| f66r | #(408.193213 434.850754) | BLACK | BLACK |
| f76r | #(826.449245 576.708765) | BLUE | BLUE |
| f85r1 | #(332.304484 377.022321) | BLACK | BLACK |
| f86v6 | #(273.050667 656.959110) | BLACK | BLACK |
| f86v5 | #(185.262918 567.980355) | BLACK | BLACK |
| f103r | #(870.000000 516.503104) | BLUE | BLUE |
| f103v | #(746.025484 660.838877) | BLUE | BLUE |
| f104r | #(299.932708 507.912599) | BLACK | BLACK |
| f104v | #(378.149001 425.497704) | BLACK | BLACK |
| f105r | #(378.065202 328.856035) | BLACK | BLACK |
| f105v | #(155.335212 348.542947) | BLACK | BLACK |
| f106r | #(388.953587 461.043067) | BLACK | BLACK |
| f106v | #(384.458624 449.601850) | BLACK | BLACK |
| f107r | #(339.797465 537.623919) | BLACK | BLACK |
| f107v | #(486.199943 609.909076) | BLACK | BLACK |
| f108r | #(644.960410 30.000000) | RED | RED |
| f108v | #(780.375010 97.074432) | RED | RED |
| f111r | #(689.717187 245.955787) | RED | RED |
| f111v | #(687.851980 807.456725) | BLUE | BLUE |
| f112r | #(531.637674 232.027928) | RED | RED |
| f112v | #(478.571649 229.115278) | RED | RED |
| f113r | #(326.889704 473.295888) | BLACK | BLACK |
| f113v | #(265.966136 518.706760) | BLACK | BLACK |
| f114r | #(281.128145 341.569104) | BLACK | BLACK |
| f114v | #(278.224695 379.583179) | BLACK | BLACK |
| f115r | #(385.985014 461.214045) | BLACK | BLACK |
| f115v | #(394.926998 411.237801) | BLACK | BLACK |
| f116r | #(774.492249 734.265683) | BLUE | BLUE |

Figure 3: PCA of biological pages with minimum spanning tree and k=3 means clustering superimposed
| Page | Coordinates | Cluster | Corrected cluster |
| f75r | #(538.086555 286.724594) | BLACK | BLACK |
| f75v | #(676.835756 280.934472) | BLACK | BLACK |
| f76r | #(302.807906 535.555547) | RED | RED |
| f76v | #(172.202236 609.675729) | RED | RED |
| f77r | #(40.843524 474.072595) | RED | RED |
| f77v | #(281.124183 598.134896) | RED | RED |
| f78r | #(575.745311 570.493862) | BLUE | BLUE |
| f78v | #(870.000000 629.180512) | BLUE | BLUE |
| f79r | #(641.270285 212.004421) | BLACK | BLACK |
| f79v | #(568.180558 258.577187) | BLACK | BLACK |
| f80r | #(491.150728 30.000000) | BLACK | BLACK |
| f80v | #(523.830709 168.465560) | BLACK | BLACK |
| f81r | #(837.068884 601.121372) | BLUE | BLUE |
| f81v | #(722.518951 542.597718) | BLUE | BLUE |
| f82r | #(70.976342 432.761396) | RED | RED |
| f82v | #(298.703237 224.852006) | BLACK | BLACK |
| f83r | #(188.842319 618.245881) | RED | RED |
| f83v | #(142.110968 420.378767) | RED | RED |
| f84r | #(482.391399 652.970607) | BLUE | BLUE |
| f84v | #(575.310148 853.252878) | BLUE | BLUE |
© Copyright Donald Fisk 2017