Macros

It will now be shown that it is possible to implement something very similar to the iterators described in the papers I wrote on Full Metal Jacket.

Macros permit behaviour which cannot be achieved even with higher-order functions. For example, instead of sending data once each time it receives data, the emit macro defined below continues to send data until its inputs satisfy a condition, the collect macro refrains from sending data until its inputs satisfy a condition, and the filter macro only sends data when its inputs satisfy a condition. Together, these can act as the components of a pipeline.

Inline Macros

Until now, iteration has been done using a single pair of start+ and repeat+ nodes, with values being updated in lockstep. It is possible in some cases to have a looser arrangement, by means of a pair of start+ and repeat+ nodes updating two values independently in separate loops. This might cause one loop to run faster than the other, resulting in either a build-up of values in input queues in the other loop or, if it runs slower, vertices on the other loop waiting for input, but it does offer more flexibility.

iterReverse can be redrawn with two separate loops as follows:

The decons node in the original implementation of iterReverse has been split up into car and cdr.

Rearranging gives us:

I have surrounded each loop. The upper loop is the master or emitter loop, and the lower loop is the slave or collector loop, with the car vertex belonging to neither loop.

A similar decoupling can be done to iterFac:

and then it, too, can be rearranged:

The emitter and collector loops cannot be made into functions, as they typically emit values several times each time they receive arguments, or collect values several times before producing outputs, and, as we shall see, they do not always emit or receive values on all of their arguments. However, they can be made into macros.

Inlining is the simplest kind of macro. When an inlined macro is used, the subgraph of vertices and edges it contains is expanded in place of the vertex containing it, so it is executed without the overhead of calling it, or returning from it.

The emitter and collector macros required for the reverse function are:




Using the above inline macros, the reverse function can now be drawn as follows:

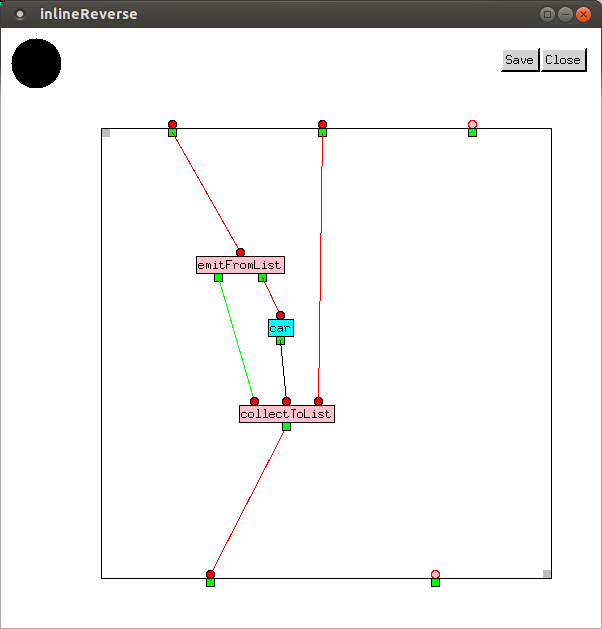
If the inputs to inlineReverse are (a b c) and (d e), the iterations are:

Similarly, the factorial function can be redrawn using inlining as follows:

With 4 as input, execution of inlineFac proceeds as follows:

Emitters and collectors can be combined in different ways. For example, to calculate the product of the numbers in a List, we could connect the emitter used in iterReverse to the collector used in iterFac. Here is the code for inlineIota, an inline version of the iota function:

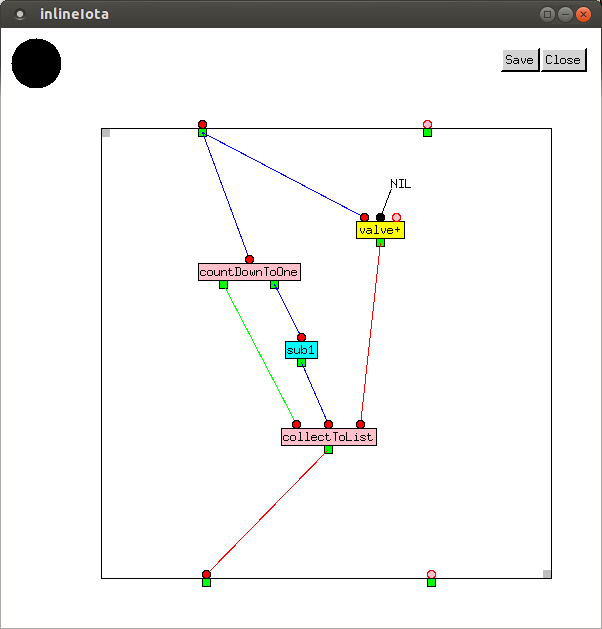
Because the contents of macros contain edges which are not connected at both ends, they can only be used inside enclosures, so they cannot be used in the sandbox.

Substitution Macros

The emitters for iterFac and iterReverse are structurally identical, and so are their collectors, so instead of using separate inline macros for each, we could use the same macros, emit and collect, for both, by supplying them with different parameter values.

The %1 vertex takes a function as its first argument. Subsequent arguments are arguments of the function. If the function is a primitive (i.e. a function written in Emblem), the %1 vertex is then replaced by a new vertex containing the code for the primitive. If it is an enclosure, the subgraph contained in the enclosure is expanded in place of the %1 vertex.

The reverse, factorial, and iota functions can now be redrawn as follows:

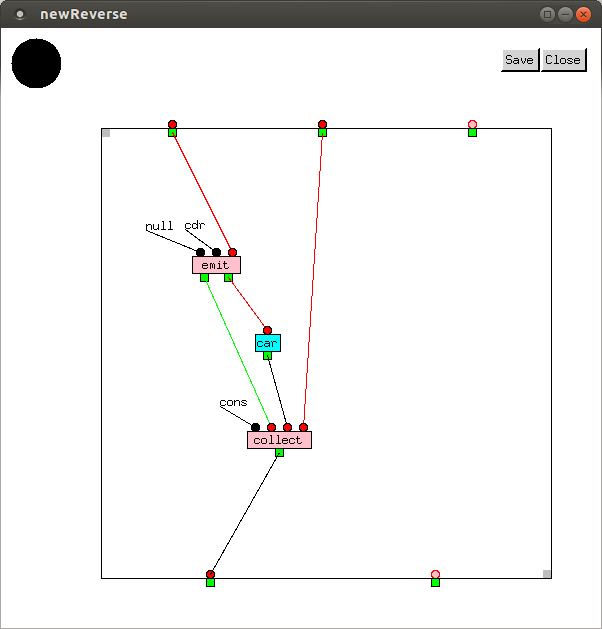
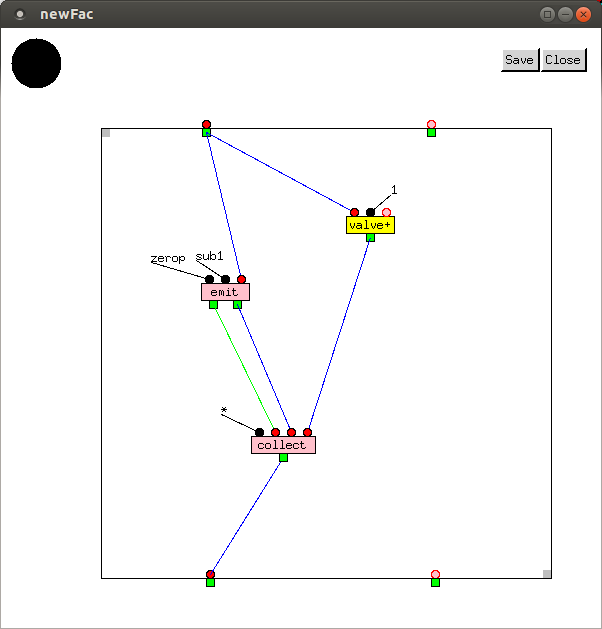
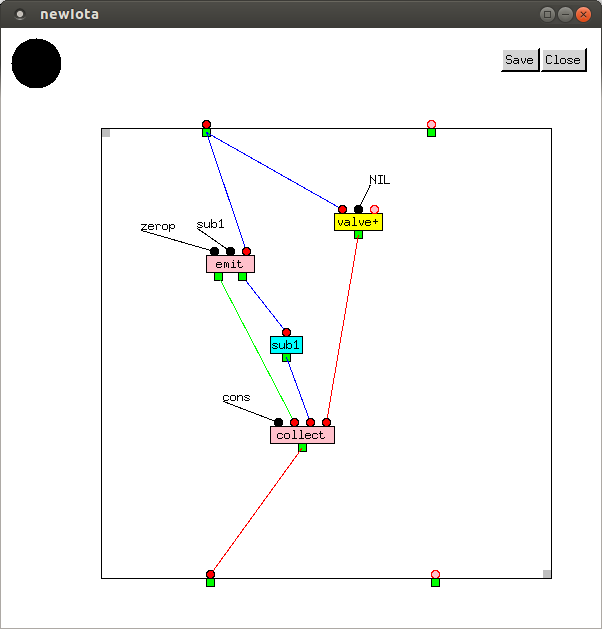
In newReverse and newIota, values are transformed after leaving emit before entering collect. Often, it is also necessary to filter values out. This can be done using the filter macro, which retains values only if the function it is supplied returns T:

Rewrite Macros

These will contain code in Full Metal Jacket, which generates a graph which replaces them, and are the most general kind of macro. They are not implemented yet.

Previous Up Next

© Copyright Donald Fisk 2015, 2016