Introduction
Handling dates isn't trivial. Here, we implement an API for the Gregorian Calendar. This isn't helpful for calculating when Chinese New Year, Passover, or Ramadan falls, but for most purposes it will suffice. The sources of complexity in the Gregorian calendar are in determining whether a given year is leap, and the different month lengths.
To simplify matters, we begin the calendar at a date
(the EPOCH) set by the user, for example Sunday, 1st January
1950. Dates before this aren't handled. The API contains three top-level
functions: indexInEpoch, which converts a given date into
the number of days from the epoch; yearMonthDay, which
converts back to a date, and dayOfWeek, which displays
the day of the week.
In the C library time.h, months start at 0 and days of the month start at 1. That is brain-damaged. Here, we will follow the ISO date convention. Months and days of the month both start at 1. Days of the week also start at 1 (Monday). Names of months and days of the week can be returned simply by array look-up.
Data Types
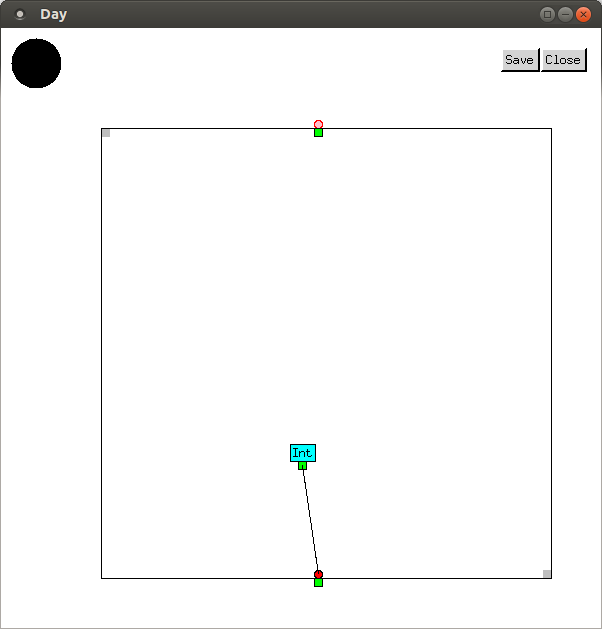
First, we define Year, Month,
and Day types. These are implemented as subtypes of
Int. This is safer than using Int, but the
extra type safety it gives us is limited. Full Metal Jacket doesn't yet
support subranges of Int, but these will be added later.


Functions
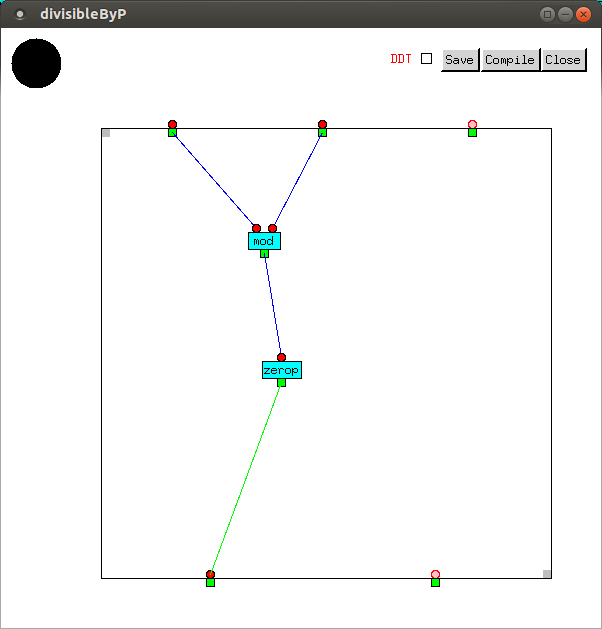
A leap year is divisible by 4, unless it's divisible
by 100 but not 400. To make the code clearer, we first define
a divisibleByP function, which outputs T if
its first input, an Int, is exactly divisible by its
second input, another Int, and otherwise outputs
NIL.
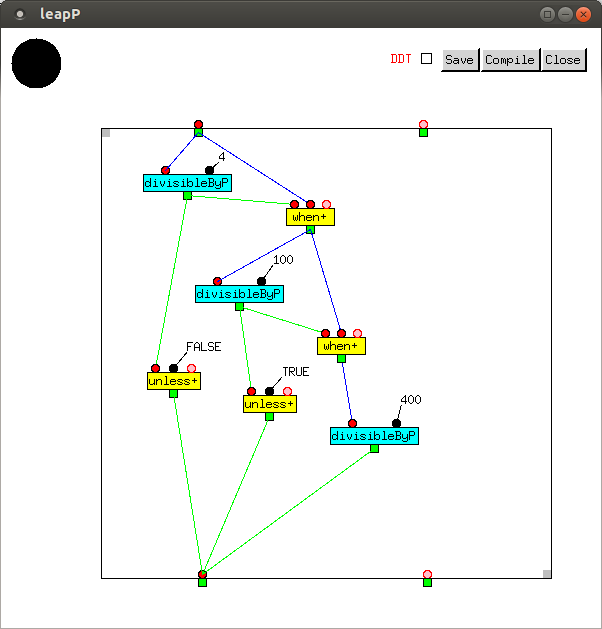
We can now define leapP, which accepts
a Year as its input, and outputs a Bool.
TRUE and FALSE are names for T
and NIL respectively, but with Boolean type.
The number of days depends on whether the year is leap.

The number of days before any month before March is the
the same in any year. From March onwards, it's one more if the year is
leap. The vector supplied to elt contains the number of days
before any month if the year isn't leap.

indexInYear returns the index of a day in a given
year, i.e. the number of days before it.

The inputs of indexInEpoch are of type
Year, Month, and Day. It outputs
the number of days from the start of the epoch.
The first value in the loop is a year, initially set to
EPOCH and incremented by one in each iteration. The second
value is the date index, initially set to 0 (its value at EPOCH),
and repeatedly incremented by the number of days in each year starting
from EPOCH. When the year which was input has been reached,
the value output by indexInYear is added to it.

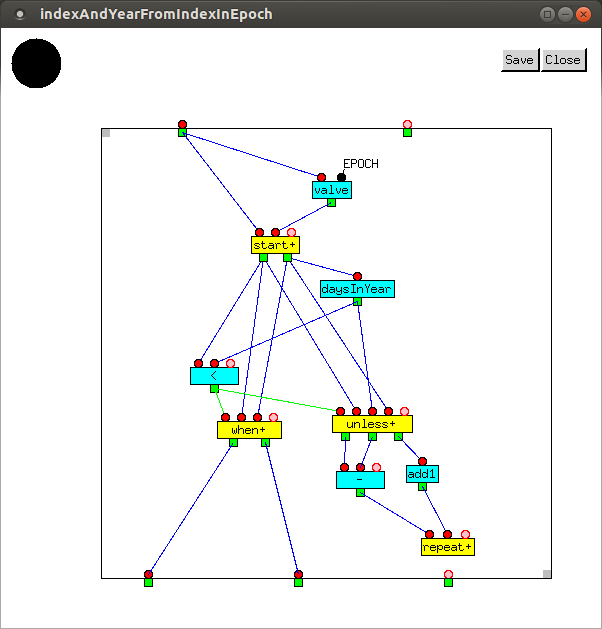
indexAndYearFromIndexInEpoch takes the number
of days since EPOCH as its input, and outputs the number
of days since new year's day, and the year.
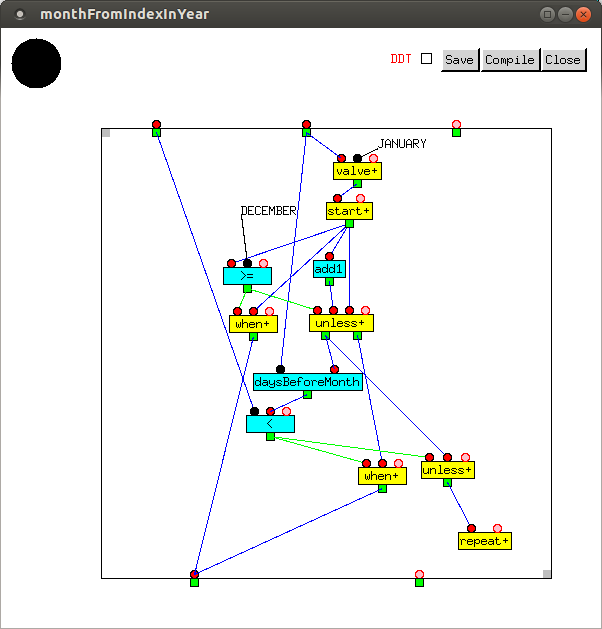
monthFromIndexInYeartakes the number of days
since new year's day and the year as its inputs, and outputs the month.
Each time around the loop, daysBeforeMonth is called, and
the value it outputs is compared against the number of days since New Year.
dayFromIndexInYear takes the number of days
since new year's day, the year, and the month, as its inputs,
and outputs the day of the month.

yearMonthDay takes number of days since
EPOCH as its input.

The day of the week is just the remainder of the number
of days since the start of EPOCH, except that it is 7 if
the remainder is zero.

In 2016, Easter falls on March 27th. It is, of course,
a Sunday. The code in the sandbox outputs the number of days since
EPOCH, then the year, month, and day of the month, followed
by day of the week.


Bell, Book, and Candle
Determining the date on which Easter falls in a given year has always been problematic. At one point, an entire branch of the early Christian Church was threatened with excommunication over of a disagreement about how to calculate it. Computus, the algorithm currently used, is quite hairy and practically incomprehensible. Even Gauss got it wrong. There have been recent attempts to introduce a simpler mechanism.
In principle, the rule for calculating Easter
is quite simple: Easter falls on the Sunday after the full moon
after the vernal equinox, which close to EPOCH generally falls
on March 20th. At the risk of being excommunicated, I will now present
a simplified algorithm, which I have to say is wrong in 2008 and 2025.
(For this, I make no apology: if ever there was a case of
accidental
difficulty, the currently accepted algorithm for Easter is it.)
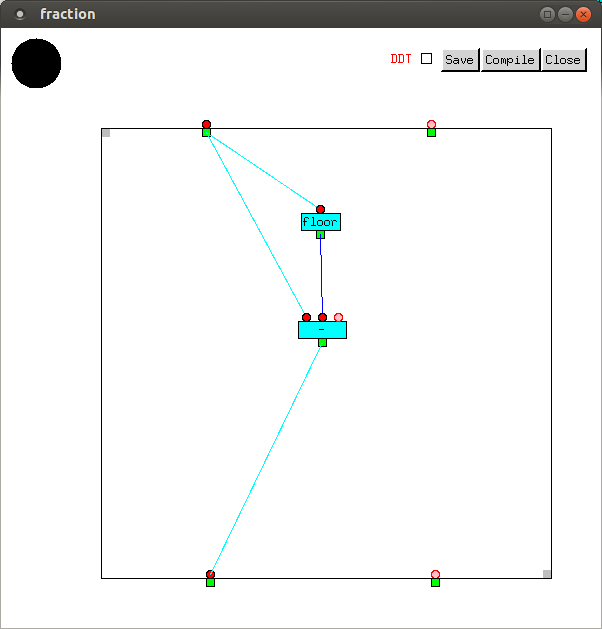
First, we write a simple helper function to calculate the difference between the value and the closest integer not higher than it.
The synodic month (i.e. the time between a given phase and
the next occurrence of it) varies only slightly, and averages
29.530588 days. So if we know the lunar phase
at the EPOCH, calculating it on any later date
is straightforward. The value returned can be any Real
between 0.0 up to but not including 1.0,
and is defined so that
| Phase | Value |
| New moon | 0.0 |
| First quarter | 0.25 |
| Full moon | 0.5 |
| Third quarter | 0.75 |

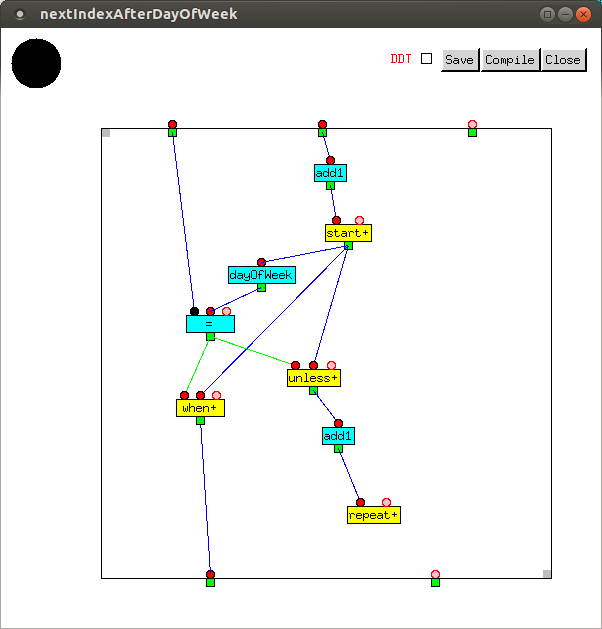
Given a day of the week (the first argument) and an index (the second argument), the next index after the day of the week is obtained by iteration, starting one day after the second argument, until the day of the week is equal to the first argument.
The day after a given lunar phase is tricky because phases
wrap around to 0.0 when a new moon is reached. This means
we should iterate starting from the difference between the lunar phase
on the day after the second argument, until 1.0 is reached
or passed, and return the index when this happens.
DAILY_LUNAR_PHASE_CHANGE is the inverse
of SYNODIC_MONTH.

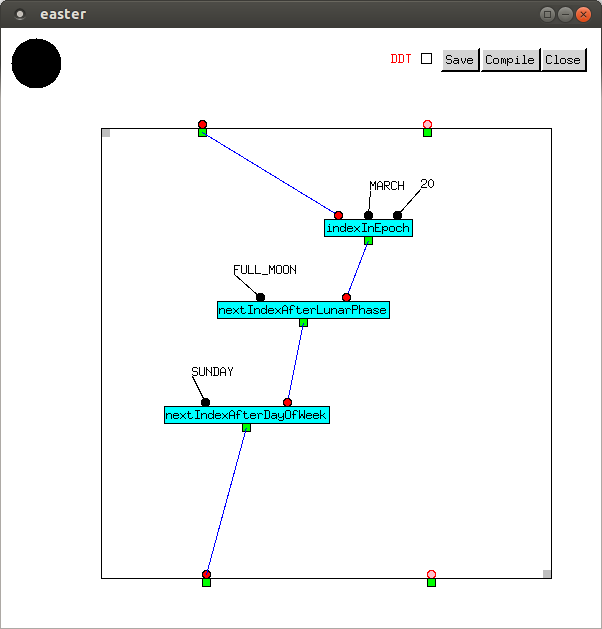
easter returns the index of the Sunday after
the full moon which follows the vernal equinox, as explained above.
The constant FULL_MOON has value 0.5.
© Copyright Donald Fisk 2016