Principal Component Analysis of Glyphs in Various Languages

Languages are written in various scripts with different glyph counts. Hawaiian has 13 letters, Chinese has thousands of characters. But Chinese characters represent whole syllables in spoken Chinese languages such as Mandarin, and sometimes several syllables in spoken Japanese. They also encode meaning, so different Chinese characters are often pronounced identically. Some other scripts (e.g. Hebrew and Arabic) omit vowels and so the same letter sequence can be pronounced in different ways.

Here, we'll mostly be examining text which is known or assumed to be alphabetic and all the sound is encoded in the written language. The choice of glyphs depends on the language and alphabet. Most European languages are written in a modified Roman alphabet, and for Latin, each letter mapped onto a single phoneme. In recent times, this is no longer true, but it is still possible to map groups of letters onto phonemes, fairly reliably in languages such as Italian, German, and Hungarian, and not so well in English and French. In what follows, a glyph is defined as comprising one or more letters corresponding to a single phoneme most of the time, or a word boundary. Examples of multi-letter glyphs include sch in German, gn in Italian, th in English, and sz in Hungarian.

The probability of a particular glyph occurring in a given place depends upon its context, and in particular the glyph preceding it. If we know, for each glyph, how frequently each glyph that can follow it occurs, it might be possible to identify the language of a text automatically, and possibly also acquire information about the pronunciation of undeciphered scripts such as the Voynich Manuscript. (This doesn't imply its contents have any meaning, only that its creators had a particular pronunciation in mind.)

The approach I'm going to take is to represent each glyph by a vector whose components depend on the frequencies of the glyphs or word ending following it. These approximately follow a Zipfian distribution, so frequently occurring glyphs will dominate, and rarer glyphs will all have similarly low values whichever glyph they follow. As this effectively reduces the dimensionality of the space spanned by the vectors, and consequently the information content of the vectors themselves, I decided to use the log frequencies instead. The precise formula used is

    a[b] = log(count(a b)) / log(count(a))
  

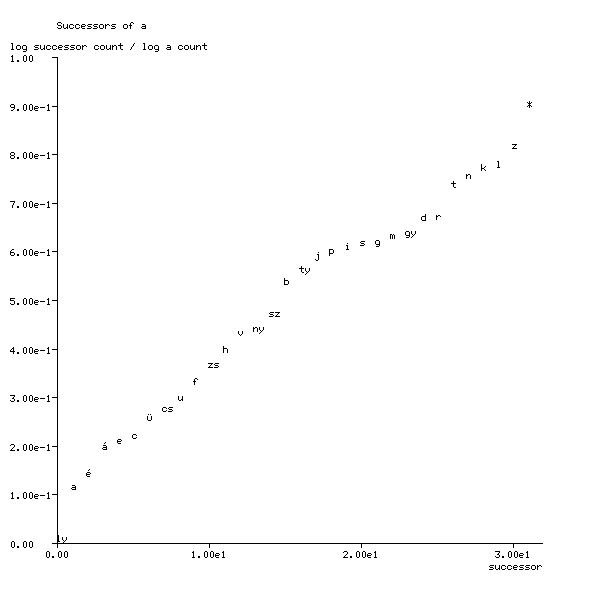
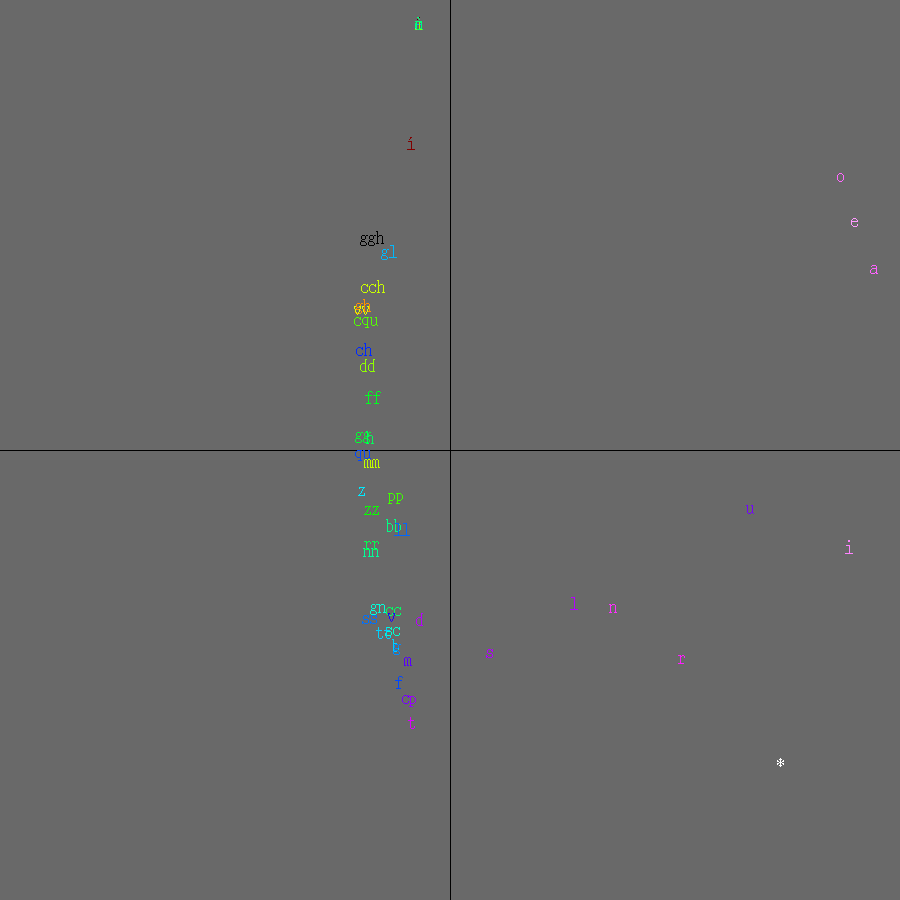
Figure 1: Successors of Hungarian a

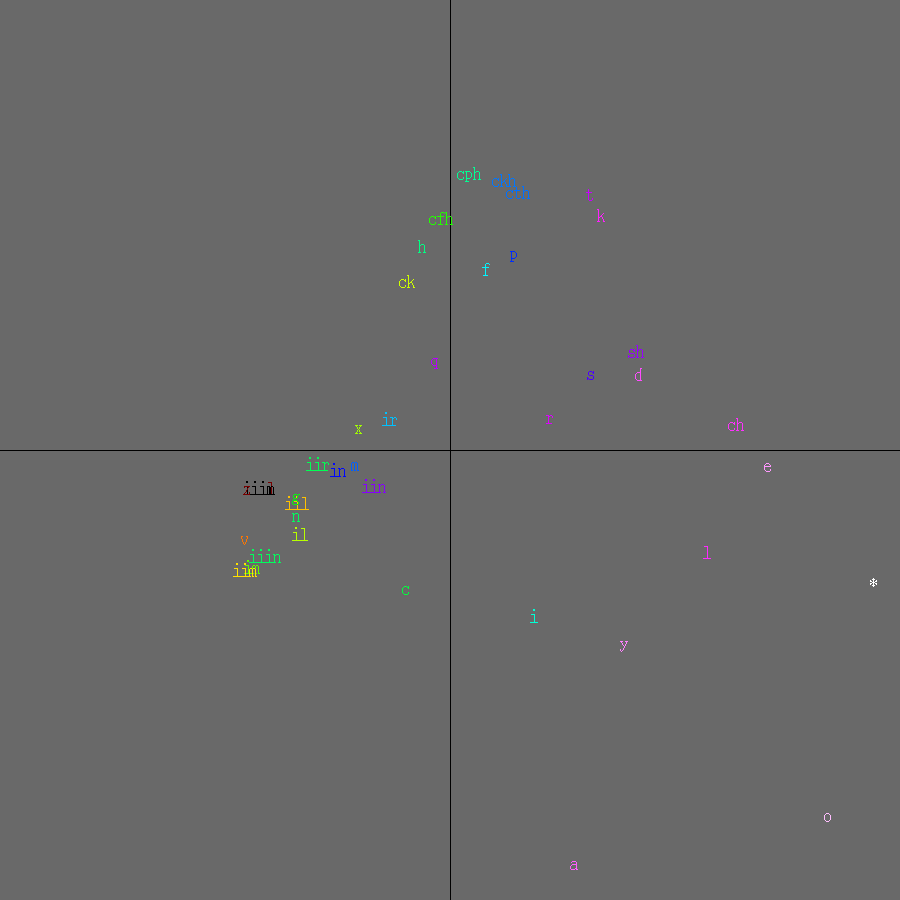
Figure 2: Successors of Hungarian f

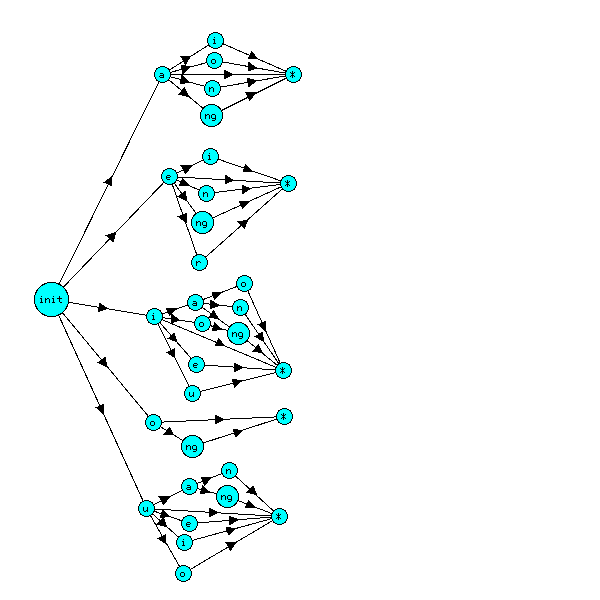
Figure 3: Successors of Hungarian sz

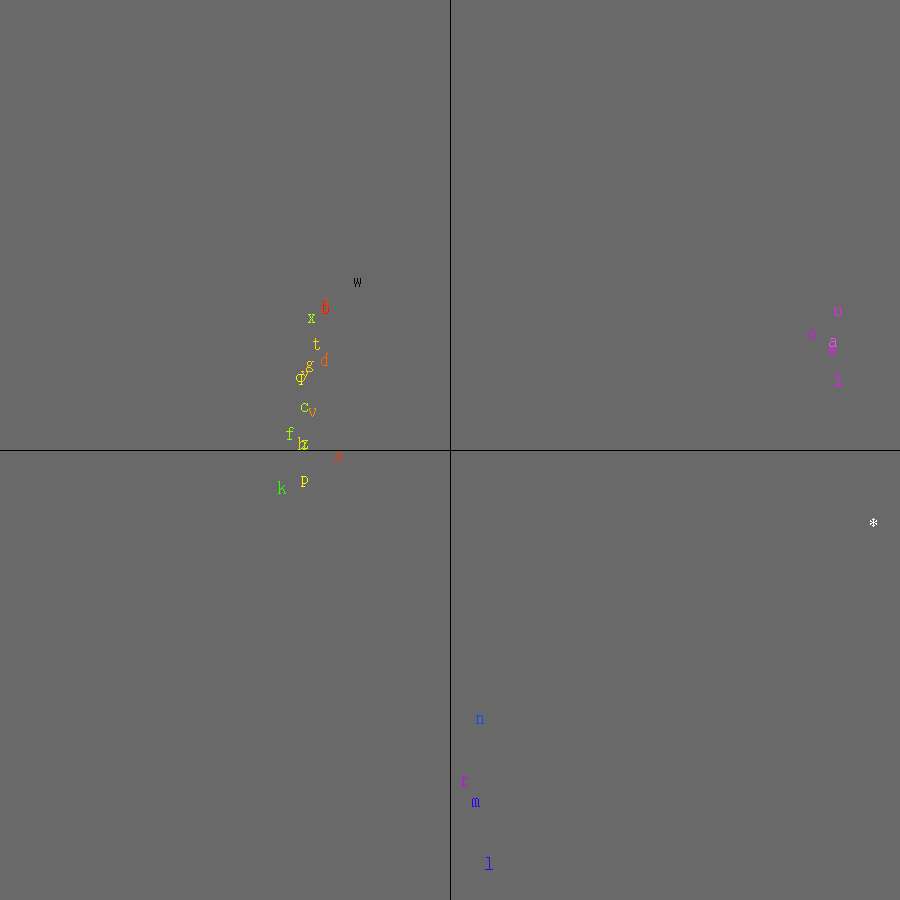
The plots in Figures 1-3 were made from the four gospels in Gáspár Károli's Hungarian translation of the Bible published in 1590. * is used for a word boundary. As can be seen, the plots are almost straight lines through the origin. This results in more information about rarer glyphs being retained. This is better for subsequent reduction to two dimensions by Principal Component Analysis (PCA), as the glyph vectors will be more evenly distributed in the glyph vector space.

The result of performing PCA on the text is shown in Figure 4:

The normalized logarithm of the glyph frequencies is indicated by color (In descending order of frequency: white, magenta, blue, cyan, green, yellow, red, black.) What is striking is that, with the exception of the rare glyphs c and Õ, the vowels and consonants separate cleanly. The word boundary is the white * at the bottom of the plot.

The vowels are close to one another in the PCA plot because, when a consonant follows a vowel, it's possible to replace it by most other consonants without affecting pronounceability much, although the vowels which can follow a particular vowel are more restricted. The result is that the vectors of the different vowels are close together in the glyph vector space.

Next is the PCA for Italian glyphs, extracted from Il Principe (The Prince) by Niccolò Machiavelli. Again, perhaps not quite as cleanly as in Hungarian, the vowels and consonants are separate. The accented vowels in Italian (shown mostly superimposed at the top of the plot) almost always occur at the ends of words, so their vector components will be close to zero except for the index corresponding to *.

The next PCA plot is for a language which most people cannot even recognize. Those I've asked guess the language is South-East Asian, possibly Thai. They were surprised it's a European language. I can recognize the script, but I cannot read it and don't even know its alphabet.

The glyphs which stand out from the rest here are ა, ე, ი, ო, უ which are a, e, i, o, and u (the language has no other vowels). This suggests it might be possible to reliably detect vowels in an unknown language using PCA. The text is from here. Don't ask me what it means.

In Figure 4, there is a cluster of consonants somewhat separate from the rest and closest to *, the word boundary, containing g, l, n, and r. In Figure 5, l, n, r, and s are found there, and in Figure 6 are მ (m), ნ (n), რ (r), and ს (s). In English and Latin texts, we find l, n, r, and s; in German text l, n, r, and t; and finally in Etruscan text l, n, and r. So it seems safe to conclude that we can also identify certain consonants with high probability.

Using PCA to detect vowels only works if the text has vowels, however, so it's unsurprising that it doesn't work for unpointed Hebrew. For Hebrew, the sofit consonants (variant forms which occur at the end of words and only rarely elsewhere) are returned where you'd expect vowels.

The next plot is for the Voynich Manuscript. We don't know how the text is supposed to be pronounced, if at all.

This time, there are no obvious vowels, but note that Italian c, f, p, t, and g, v, b, d occur in similar places o Voynichese k, f, p, t, and ckh, cfh, cph, cth. (PCA plots can be rotated or reflected and mean the same.) Voynichese a and o are roughly in the correct place to be vowels. c, i, and y might also be vowels.

Because Voynichese looks so odd, I decided to analyse a phonetically more exotic language, Mandarin Chinese. Words in Mandarin comprise one or more syllables, which have a simple internal grammar. Syllables have one of five different tones.

Figure 8: Structure of Mandarin/Pinyin syllables

init can be either a single consonant (b, p, m, f, d, t, n, l, g, k, h, j, q, x, z, h, ch, sh, r, z, c s, w, or y) or null.

Pinyin text with tones indicated by accent marks can be found at Pīnyīn Rìjì Duǎnwén. I corrected d to de (的) and ran a PCA:

Two things are interesting here. As you'd expect, glyphs of same vowel with different tones occur close together, and the large number of vowel variants cause the vowels and consonants to move apart (to keep the centre of gravity at the centre of the plot). i and u are apart from the other vowels, an artifact caused by the placing of tones on diphthongs.

As this looked different from most other languages I've examined, and vaguely resembles the Voynichese plot, although no variety of Chinese is plausible as the Voynich Manuscript's plaintext language, I decided to plot Latin with long and short vowels indicated, a sample of which I found at Ovidii Metamorphoses. Latin is one of the three most likely languages if the text is meaningful (the other two being German and Italian).

This also vaguely resembles the Voynichese plot. The problem is that Voynichese doesn't seem to have too many characters where you'd expect vowels, so the trick I applied to Chinese and Latin wouldn't work.

How to interpret the PCA glyph plots

Each glyph can be represented as a point in an n-dimensional space whose coordinates are the normalized log frequencies of the glyphs which occur next in the text. Principal component analysis reduces the number of dimensions, here to two, while retaining as much information as possible, by projecting the points onto a plane. The orientation of a PCA plot is unimportant, and as they are demeaned the centre of the plot is at the centre of gravity of the glyphs.

On each plot, vowels are usually close to one another, and separate from consonants, because the letters following each vowel tend to have similar frequencies. Replacing a vowel with a different vowel in a word rarely affects pronounceability (except perhaps where it's the first vowel of a diphthong).

Only certain combinations of phonemes are easily pronounceable, so these appear in natural languages. Usually, syllables are consonant-vowel. Sometimes the initial consonant is missing, or is replaced by a consonant cluster (like str in English). Sometimes there are dipthongs instead of single vowels. Sometimes there's a consonant or consonant cluster after the vowel, like in stand. Sometimes a liquid consonant can replace the vowel in a syllable, e.g. the final l in little.

To show how all of this affects PCA glyph plots, we can invent arbitrary languages with specific phonetic properties and generate PCA glyph plots for them. Firstly, we see what happens when letters are distributed randomly, such as you might get by using a modern encryption technique. The text looks like this:

The plot is just a random distribution of points.

Next is a language whose syllables are always consonant-vowel. Some languages, such as Japanese, closely follow this pattern. The text looks like this:

This time, the vowels and consonants separate. Consonants can only be followed by vowels, and vowels and space by consonants.

Finally, consonant-vowel-liquid. This looks more like European languages even if it's still gibberish:

Now, there's an additional cluster corresponding to the liquids.

For a number of reasons, most plots don't faithfully adhere to the last two patterns, though Italian comes close: scripts are rarely exactly phonetic, even where they are the rules are often complex and context-dependent so you can't reliably map glyphs onto phonemes, and languages evolve so that specific consonant clusters, diphthongs and consonant-vowel pairings are preferred (e.g. nd over md).

Effect of encryption on PCA glyph plots

The cryptographic techniques used in Europe at the time the Voynich Manuscript was created weren't very sophisticated (Fifteenth Century Cryptography). They were

1. Simple substitution. This is replacing one glyph with another. The PCA glyph plot would be unchanged, except each glyph would be replaced by a different one.
2. Homophones. These replace each vowel with multiple glyphs with the intention of making it more difficult to tell vowels from consonants. If the replacement glyphs are selected randomly, in place of each homophone there would be several glyphs very close to one another on the PCA plot, because the following letter frequencies will be unaltered.
3. Nulls. These are glyphs inserted into the text which are simply ignored. If the nulls are randomly inserted, they will appear close to one another on the PCA glyph plot, around the centre of gravity of the glyphs.
4. Nomenclators. These are codes, e.g. substituted for names and other words. It's difficult to say what their effect would be. How much effect these have on a PCA glyph plot depends on how many are used.

As far as I can see, none of these techniques could reshape the plot for Italian, or any other language with the usual repertoire of vowels, into anything resembling the plot for the Voynich Manuscript.

There are, though, some things which could be tried: e.g. merging two or more EVA glyphs into a single glyph, disregarding spaces, treating EVA glyphs as nulls or spaces, and repeating the process until the PCA plot resembles a known language, or at least has separate consonant and vowel branches.

And Finally

I did find a text with a glyph cloud similar to that of the Voynich Manuscript:

The only problem is that nobody knows which language it's written in either. I used the transcription at Rohonc Transcription and omitted glyphs occurring less than 50 times.