Voynich State Transitions

One of the most surprising things about the Voynich Manuscript is that the glyphs within words follow a clearly discernible grammar, yet the words in sentences don't. (In fact, as there's no punctuation, where sentences begin and end, or whether they exist at all, is unclear.)

All the prefixes in Table 1 and Table 2 in The Structure of the Words in the Voynich Manuscript can be generated by traversing this state transition diagram:

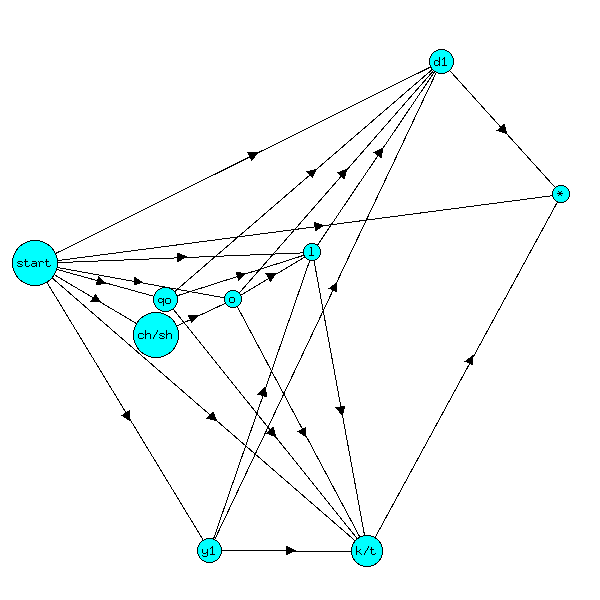
Figure 1: State transition diagram for common prefixes

All the suffixes in Table 2, Table 4, and Table 6 can be generated by traversing this one:

Figure 2: State transition diagram for common suffixes

NB * isn't really a state in either diagram. Ideally, the two diagrams should be merged into a single diagram, and any state in Figure 1 with a transition shown to * has transitions to all of the states in Figure 2 with transitions shown from *.

q and o are normally considered separate glyphs, but q is only very rarely followed by anything other than o, so I have merged the two glyphs into a single glyph, qo.

The diagrams are simplified in a number of ways. States with the same precursor and successor states are merged, e.g. k/t is really two states, k and t, and a/o is a and o2. Numbered states, e.g. y1 and y2, both output the same letter but occur more than once. Finally, iX indicates endings such as iin and ir.

For example, daiin can be generated by traversing the states

and qokeedy by traversing the states

How it is decided which transition to taken from any state to the following one isn't at all obvious, but one possibility that should be considered is that it is random, possibly with different probabilities attached to each transition. This would mean that the text is meaningless, though it is possible that following a transition merely appears to be random, e.g. as a result of a previous encryption step, and it would be difficult to tell the two possibilities apart. However, it would render untenable the ideas that the manuscript is either plaintext in an unidentified language or non-verbose cyphertext.

Transition Probabilities

From any state, the transition probabilities can be reverse engineered by incrementing the count for the next transition leading to a state which writes the following glyph and then moving to that state, or backtracking (and decrementing the count) whenever no such state is found, and then following an alternative path from the last decision point. When this is repeated for the entire text, the probabity for a transition from a state are the number of times the transition has been traversed divided by the number of times any transition from that state has. As word frequencies vary throughout the manuscript, this will have to be done section by section.

For the blue herbal pages, the number of occurrences of words with the common prefixes and suffixes is shown in Table 1. Note that one word, dy, occurs twice, as -dy and again as d-y.

The state transition table derived from the blue herbal pages, and limited to common prefixes and suffixes, is shown in Table 2. The first column is the state ID. The second is the glyph to be printed when the state is reached, and the subsequent columns are the per mille probabilities of the next state. Very small probabilities are shown as ε, and zero probabilities are not shown.

Note that Table 2 is a single table, without any boundary between prefixes and suffixes.

To generate a word, begin at the row for the start state. Make a weighted random choice from among the entries, and then move to the row for the corresponding state, and repeat until the finish state has been reached.

Making a weighted random choice is easy to do on a computer, but how could it have been done quickly in the early 15th Century? Dice are unsuitable. The scribe would have had to throw at least two, and then do some mental arithmetic before being able to select the next state. A much easier way would be to shuffle a deck of playing cards and draw each card in turn. This gives 52 possibilities if the suits are ordered. If the probabilities in each state transition table were entered cumulatively as particular cards in the deck, our scribe could search along the row until one with a higher card value is found, choosing the next state that way, which would be quite fast.

According to Early references to Playing Cards, playing cards were introduced into Europe in the late 14th century, and became popular over the next few decades. Tarot cards appeared by 1440, and might have been used instead.

The state transition diagram in Table 2 was then used to predict the number of occurrences of words, resulting in Table 3.

The RMS error on the non-zero values in either the Table 1 or Table 3 is 1.933788. A different state transition table was generated for each section, and the RMS errors of the predicted word counts were calculated as before. The results are shown in Table 4.

Table 4: RMS errors for non-zero values of predicted word counts

Table 5 and Table 6 show the state transition diagrams for two further sections, red text and blue biological.

With the existing state transition tables, less than 40% of the words can be generated, but it is possible to extend them to handle most if not all of the text.