Prime Number Computation

Collecting the primes

sieve returns a list of prime numbers up to its argument, n. It starts with a queue containing just the value 2, and iterates through odd numbers from 3 until n is reached. Any which are found to be prime are added to the end of the queue. A queue is used instead of a list to ensure that values in the returned list are in the correct order.

In the Lisp dialect Emblem, this is:

(defun sieve (n)
  (do ((i 3 (+ i 2))
       (q (queueFromList (list 2))
          (if (primeP i (elemsOfQueue q))
              (putOnQueue i q)
            q)))
      ((< n i) (elemsOfQueue q)))))

Balancing the inputs

By inspection, it can be verified that each vertex's inputs receives the same number of values, as follows:

Senders	Input Count	Vertex	Output Count
ingate	1	`valve+`	1
`valve+`	1	`list`	1
`list`	1	`queueFromList`	1
`valve+` `queueFromList`	1	`start+`	N
ingate `start+`	N	`<`	N
`<` `start+`	N	`when+` (from `<`)	1
`<` `start+`	N	`unless+` (from `<`)	N-1
`when+`	1	`elemsOfQueue`	1
`unless+`	N-1	`+`	N-1
`unless+`	N-1	`elemsOfQueue`	N-1
`unless+` `elemsOfQueue`	N-1	`primeP`	N-1
`primeP` `unless+`	N-1	`when+`	P
`primeP` `unless+`	N-1	`unless+`	N-1-P
`when+`	P	`putOnQueue`	P
`+` `putOnQueue` and `unless+`	N-1	`repeat+`	0

Bugs to avoid

The likeliest bug is not feeding back the unaltered queue in the slave loop if the number isn't prime. Next, if the second input of > in the master loop is not sticky, it would only execute once, as it is injected into the loop from outside and would be immediately consumed. Thirdly, as list structure used in the queue of primes is destructively modified (added to) when putOnQueue is called, it is essential to initialize it with a fresh list by calling list. Finally, it is important to verify that the inputs on each vertex are balanced.

Testing the primes

The first input value of primeP is the number being tested, and the second is the list of primes less than it. As primeP is only required inside sieve, it only needs to test numbers which haven't been tested yet. As all the numbers less than the number we're currently testing will already have been tested, we already have all the primes we need. (Actually more than we need, since when testing a number for primeness, we only need primes up to its square root.)

primeP iterates through the list of primes, and if one exactly divides the number (its remainder is zero), the number is not a prime, and primeP returns NIL. Otherwise, if a prime squared is greater than the number, we've checked all the primes on the list we need to, and none was an exact divisor, so we return T.

For clarity, in the Lisp shown below, the expression (zerop (mod i (car primes))) to test if the remainder is zero was repeated. A temporary variable could have been used instead. In the Full Metal Jacket code, we simply added another edge from the not vertex. Finally, two sticky values were needed as a value was being injected into a loop.

(defun primeP (i listOfPrimes)
  (do ((primes listOfPrimes (cdr primes)))
      ((or (zerop (mod i (car primes)))
           (> (* (car primes) (car primes)) i))
       (not (zerop (mod i (car primes)))))))

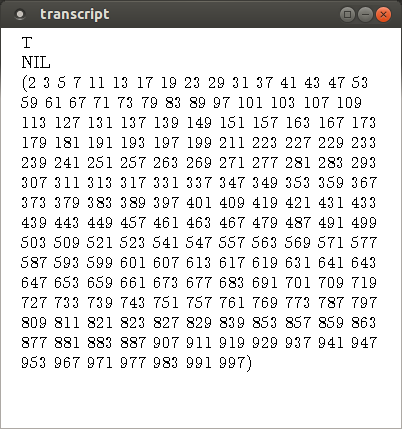
Two call to primeP, followed by one to sieve are shown, followed by their output.

Previous Up Next